Overview
In second grade, students in SFUSD engage in 60 minutes of daily math instruction. Math instruction supports students in building agency and supports their identities as mathematicians. Math lessons provide both concrete and conceptual understanding for students by giving them opportunities to deepen their understanding of concepts through play and exploration. By the end of the year, second-grade students fluently add and subtract within 100 and know all sums of two one-digit numbers from memory.

During math instruction, students are engaged in a number of instructional contexts and routines: math talks, counting routines, and learning stations. Math talks feature flexibility with numbers and developing understanding of the base 10 system, and developing strategies such as repeated counting of groups of objects such as coins or objects arranged in arrays. In addition, engaging in collaborative tasks and games will result in joyful math learners.
Overview Link to this section
|
Mathematics* |
60 mins every day |
|---|---|
|
Counting & Daily Routines |
10 mins every day. May or may not be connected to the lesson |
|
Math Talk |
10-15 mins, 3-5 days per week. May or may not be connected to the lesson |
|
Lesson |
20 mins every day |
|
Learning Stations |
10-20 mins, 3-5 days per week. May or may not be connected to the lesson |
*The components listed may be taught at different times of the day (i.e. Extend your Morning Meeting to include daily routines).
Priority Standards Link to this section
What students will know, what students will do, and what thinking skills students will develop to apply and transfer mathematical understandings that endure within the discipline, leverage deeper understandings, and/or support readiness for success at the next grade level.
In Second Grade focus on these critical areas:
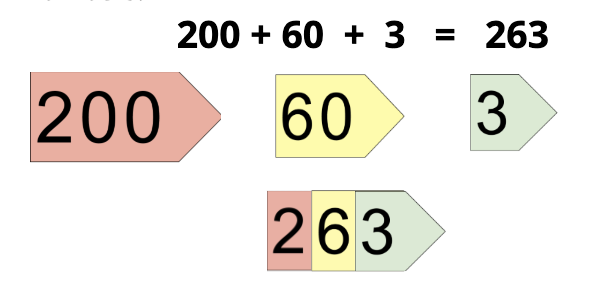
Extending Understanding of Base-Ten Notation
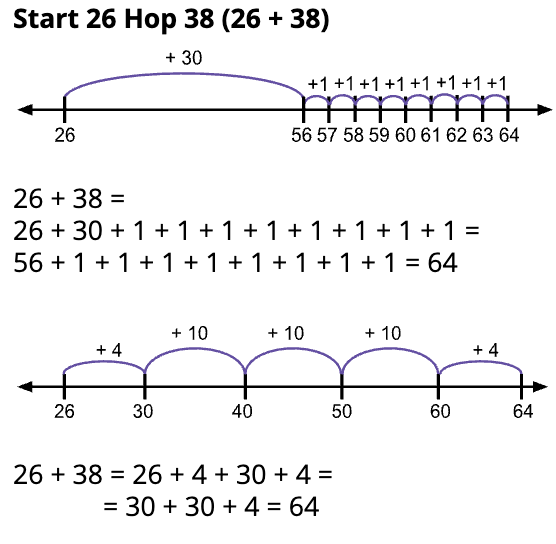
Building Fluency with Addition & Subtraction
The second-grade fluency requirements are single-digit sums and differences and adding and subtracting within 100.
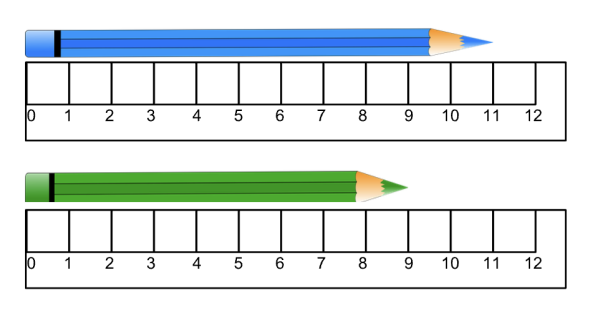
Using Standard Units of Measure
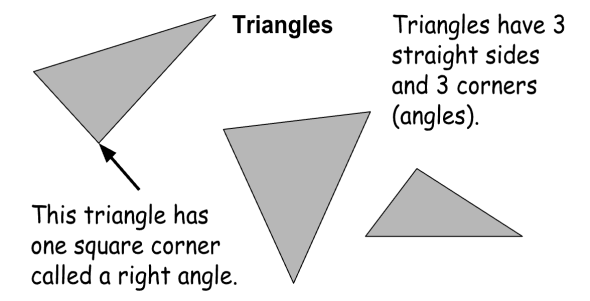
Describing & Analyzing Shapes
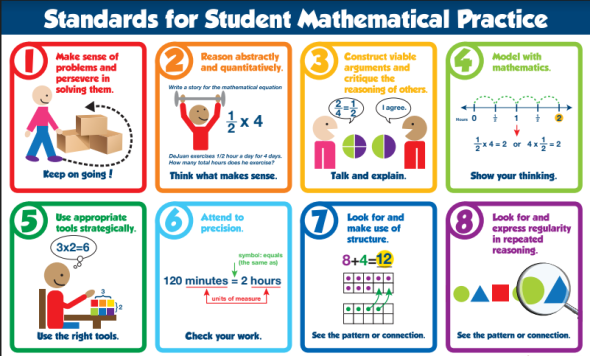
Behaviors of Mathematicians
In addition to grade-specific content standards, all grades K-12 share the same 8 Standards for Mathematical Practice that describe the behaviors of mathematicians.
- Make sense of problems and persevere in solving them
- Reason abstractly and quantitatively
- Construct viable arguments and critique the reasoning of others
- Model with mathematics
- Use appropriate tools strategically
- Attend to precision
- Look for and make use of structure
- Look for and express regularity in repeated reasoning
Instruction: Signature Elements Link to this section
Below are signature elements of SFUSD Math instruction that students should experience regularly throughout Kindergarten as they develop as mathematicians.
Math Norms
Class norms help students, and give them opportunities to be accountable to the community and to act on the prosocial values of responsibility, respect, fairness, caring, and helpfulness. They support equitable participation, engagement with the practices of doing math, and the establishment of a positive classroom climate. Establish class norms at the beginning of the school year and continue to reinforce them every day.
Math Talks
Math Talks are teacher-led, student-centered techniques for building math thinking and academic discourse. They allow for multiple entry points and encourage students to value the thinking of others so that they can build a better understanding of their own thinking. Math Talks support students in developing their mental math skills.
Three Read Protocol
The Three Read Protocol is one way to do a close read of a complex math word problem or task. This strategy includes reading a math scenario three times with a different goal each time. The first read is to understand the context. The second read is to understand the mathematics. The third read is to elicit inquiry questions based on the scenario.

Groupwork Feedback
Groupwork feedback is a strategy to publicly recognize the class norms and math focus of students as they work in groups. Groupwork is loosely defined to include partners, trios, or larger group sizes. The teacher takes public notes about the quality of the group work and the quality of the mathematical discussions. This feedback should focus on the specific nature of group work interactions as well as target mathematics of the lesson rather than general positive reinforcement.

Routines
Daily routines are the cornerstone of the mathematics curriculum in the early primary grades. This structure provides opportunities for deeper learning that requires students to continuously revisit potentially abstract concepts in a concrete context. Although the basic routine structures will stay the same throughout the year, the complexity and focus will change and develop over time.
Learning Stations
Learning stations are an activity-based structure that provides students with opportunities for student-led engagement with, or extensions of, previously taught concepts. Stations can also be used to explore new manipulatives/tools before they are used in a formal lesson. You can use this time to observe students, pull small groups for targeted instruction or formative assessment, or teach the lessons in small groups.
Materials
Below are items you should have to support your students' Math instruction. If you are missing anything from the list, please first contact your site administrator or designated support. If they are unable to resolve the issue promptly, please contact your site’s liaison from the C&I Math Department.
Student Classwork and Homework booklets are centrally printed and provided by the SFUSD Math Department. Here are PDFs of the Student Pages.
Manipulatives have already been provided to each site and should remain with the classroom. Here is a list of manipulatives for each grade Pre-K through 5.
Units
Unit Design
SFUSD units are designed around four tasks. These tasks offer all students opportunities to engage in meaningful and rigorous mathematics that allow for the development of the Standards for Mathematical Practice. These tasks give information about how students are learning the core concepts and skills of the unit.
All tasks are used for formative assessment—gathering information about what students know and are able to do—but these tasks are not tests. The Entry, Apprentice, and Expert Tasks allow for student collaboration and individual accountability without being graded based on an expectation of mastery. The Milestone Task can be used as an individual assessment for grading students.
 |
|---|
- Entry Task: What do you already know?
- Apprentice Task: What sense are you making of what you are learning?
- Expert Task: How can you apply what you have learned so far to a new situation?
- Milestone Task: Did you learn what was expected of you from this unit?
Units
| Unit | Description | Orientation | |
|---|---|---|---|
| The first week of school is focused on setting up the heterogeneous classroom and culture for the year and developing routines that support the development of the Standards for Mathematical Practice. | |||
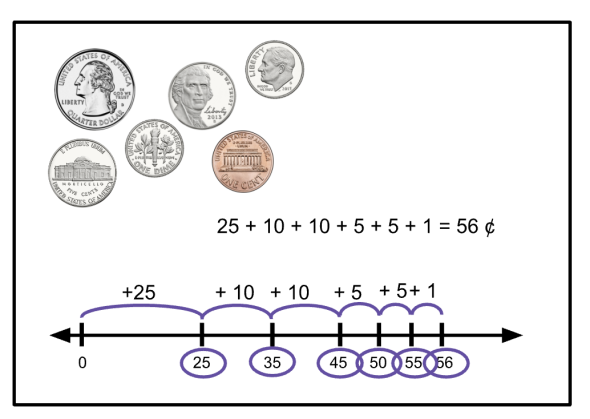
| A collection of objects can be put into equal groups of 2s, 5s, and 10s. Coins come in denominations of 1¢ (penny), 5¢ (nickel), 10¢ (dime), and 25¢ (quarter). | Unit 2.1 Orientation | ||
| Lengths can be estimated, measured, and compared using inches, feet, centimeters, or meters. The longer the unit of measure, the fewer units it takes to measure an object. | Unit 2.2 Orientation | ||
| Numbers can be combined by thinking about the values of their digits, combining tens with tens and ones with ones, and sometimes composing 10 ones into 1 ten. | Unit 2.3 Orientation | ||
| Time can be expressed using different units that are related to each other. Telling time requires an understanding of the relationship between minutes and hours. | Unit 2.4 Orientation | ||
| Numbers can be subtracted by thinking about the values of their digits, subtracting tens from tens and ones from ones, and sometimes decomposing 1 ten into 10 ones. | Unit 2.5 Orientation | ||
| Real-life situations can be represented by addition and subtraction equations with unknowns in any position. We can solve them using understanding of place value and the meaning of operations. | Unit 2.6 Orientation | ||
| Just as 10 ones make 1 ten, 10 tens make 1 hundred, and 10 hundreds make 1000. Counting, writing, and comparing numbers greater than 100 requires understanding of the value of each place. | Unit 2.7 Orientation | ||
| Numbers can be added and subtracted by thinking about the values of their digits. When adding or subtracting three-digit numbers, one adds or subtracts hundreds and hundreds, tens and tens, ones and ones; and sometimes it is necessary to compose or decompose tens or hundreds. | Unit 2.8 Orientation | ||
| Shapes can be described uniquely by their attributes, such as the size and shape of their sides and angles. Shapes can be composed and decomposed to make new shapes. | Unit 2.9 Orientation | ||
| Two-step problems involving adding to, taking from, joining, separating, and comparing can be solved with addition and/or subtraction. | Unit 2.10 Orientation | ||
| Categorical and numerical data can be collected, recorded, and organized. There are various ways to represent, display, describe, and interpret data using tables and graphs. | Unit 2.11 Orientation |
Lesson Structure and Core Math
|
LAUNCH |
The launch of a lesson or task is a brief hook that might relate to previous learning, establish an inquiry question, or connect to real-world situations or interests. It will also support students to understand what is being asked of them, which may include guidance on the use of materials such as manipulatives. |
|
Key Questions How can you connect to students' interests/lives (hook)? |
|
|
EXPLORE |
During the Explore part of a lesson or task, students carry the cognitive load. Students experiment together with the most important math of each unit to develop, deepen and secure their mathematical understanding. Students represent their thinking by using numbers, words, pictures, and/or visuals; an example of a visual representation would be an array or a number line. Students are talking throughout this part of the lesson and build on each other’s ideas and questions. The Explore often includes a math game. |
|
Key Questions What are students doing? What work do you want to highlight? What does their work show about what they understand? What language are the students using to describe their work? |
|
|
SUMMARIZE |
During the Summarize part of a lesson or task, the teacher facilitates a conversation where students share what they have learned related to the core math. They notice and name similarities, differences, or connections across several different pieces of math work. A summary often, but not always, includes routines for consolidation of learning, such as a gallery viewing or individual reflection in a notebook. |
|
Key Questions How will you sequence the work to elicit peer-to-peer academic discourse?
|
Planning Guide
This calendar is intended as an instructional guide to help with year-long planning. There is no expectation that you teach a particular lesson on a particular day. Each unit is set within a “window” of time that gives you some flexibility.
Reflection Questions Link to this section
- How are students' developmental needs, communities, and experiences being reflected and honored, or how could they be?
- What opportunities do you see for developing equitable access & demand, inquiry, collaboration, and assessment for learning?
- What are the implications for your own practice? What strengths can you build upon? What will you do first?
Want More?
Standards
More Resources
- The SFUSD Math Core Curriculum Second-Grade Overview includes the priority standards, the scope and sequence of units and standards, the unit design, class norms, key instructional strategies, and icons used throughout the curriculum to support planning.
- Assessment resources (in addition to the embedded formative assessment in the Core Curriculum)
Contact the Math Team:
This page was last updated on May 18, 2023

