Overview
Link to this section
First-grade students engage in 50-60 minutes of daily math instruction that provides a strong sense of agency and supports their identities as mathematicians. Through play and exploration, math lessons develop conceptual understandings about the relationship between addition and subtraction, and the idea of 10 ones as a new unit called a ten. Students also develop procedural fluency within 10.
During math instruction, students are engaged in a number of instructional contexts and routines: math talks, counting and calendar routines, and learning stations. Math talks feature subitizing (recognizing a number of objects without counting) and flexibility with mental math strategies such as counting on; making ten, and decomposing a number leading to a ten. In addition, engaging in games and collaborative tasks will result in joyful math learners.
Overview Link to this section
|
Mathematics* |
50 mins every day |
|---|---|
|
Counting & Daily Routines |
10 mins every day. May or may not be connected to the lesson |
|
Math Talk |
10-15 mins, 3-5 days per week. May or may not be connected to the lesson |
|
Lesson |
20 mins every day |
|
Learning Stations |
10-20 mins, 3-5 days per week. May or may not be connected to the lesson |
*The components listed may be taught at different times of the day (i.e. Extend your Morning Meeting to include Counting and Daily routines in the form of daily calendar).
Priority Standards Link to this section
What students will know, what students will do, and what thinking skills students will develop to apply and transfer mathematical understandings that endure within the discipline, leverage deeper understandings, and/or support readiness for success at the next grade level.
In first grade focus on these critical areas:

Developing understanding of addition, subtraction, and strategies for addition and subtraction within 20
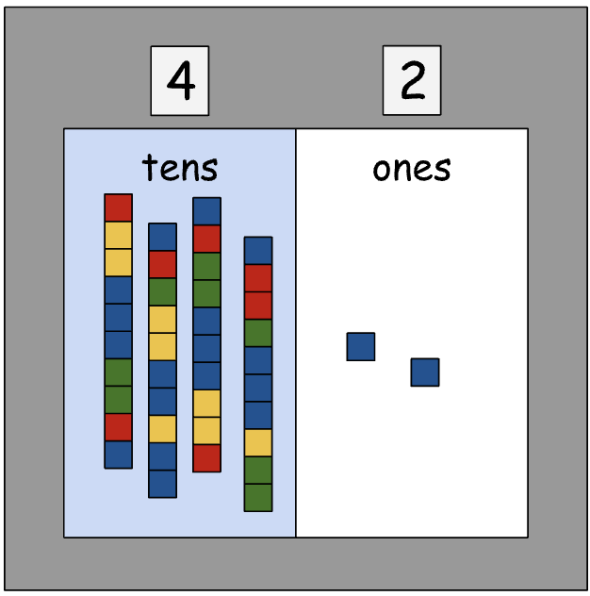
Developing understanding of whole number relationships and place value, including grouping in tens and ones

Developing understanding of linear measurement and measuring lengths as iterating length units

Reasoning about attributes of, and composing and decomposing geometric shapes
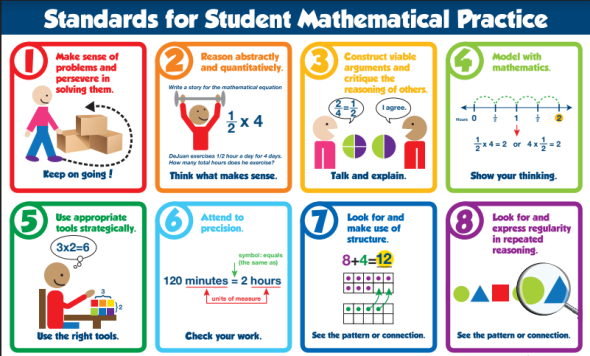
Behaviors of Mathematicians
- Make sense of problems and persevere in solving them
- Reason abstractly and quantitatively
- Construct viable arguments and critique the reasoning of others
- Model with mathematics
- Use appropriate tools strategically
- Attend to precision
- Look for and make use of structure
- Look for and express regularity in repeated reasoning
Instruction: Signature Elements Link to this section
Below are signature elements of SFUSD Math instruction that students should experience regularly throughout First Grade as they develop as mathematicians.
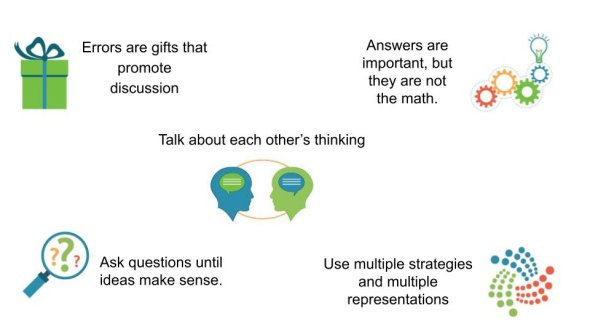
Math Norms
- Answers are important, but they are not the math
- Talk about each other's thinking
- Errors are gifts that promote discussion
- Ask questions until ideas make sense
- Use multiple strategies and multiple representations
Math Talks
Math Talks are teacher-led, student-centered techniques for building math thinking and academic discourse. They allow for multiple entry points and encourage students to value the thinking of others so that they can build a better understanding of their own thinking. Math Talks support students in developing their mental math skills.
Three Read Protocol
The Three Read Protocol is one way to do a close read of a complex math word problem or task. This strategy includes reading a math scenario three times with a different goal each time. The first read is to understand the context. The second read is to understand the mathematics. The third read is to elicit inquiry questions based on the scenario.

Groupwork Feedback
Groupwork feedback is a strategy to publicly recognize the class norms and math focus of students as they work in groups. Groupwork is loosely defined to include partners, trios, or larger group sizes. The teacher takes public notes about the quality of the group work and the quality of the mathematical discussions. This feedback should focus on the specific nature of groupwork interactions as well as target mathematics of the lesson rather than general positive reinforcement.

Routines
Daily routines are the cornerstone of the mathematics curriculum in the early primary grades. This structure provides opportunities for deeper learning that requires students to continuously revisit potentially abstract concepts in a concrete context. Although the basic routine structures will stay the same throughout the year, the complexity and focus will change and develop over time.

Learning Stations
Learning stations are an activity-based structure that provides students with opportunities for student-led engagement with, or extensions of, previously taught concepts. Stations can also be used to explore new manipulatives/tools before they are used in a formal lesson. You can use this time to observe students, pull small groups for targeted instruction or formative assessment, or teach the lessons in small groups.
Materials
Below are items you should have to support your students' Math instruction. If you are missing anything from the list, please first contact your site administrator or designated support. If they are unable to resolve the issue promptly, please contact your site’s liaison from the C&I Math Department.
SFUSD Math Student Classwork and Homework booklets are centrally printed and provided by the SFUSD Math Department; the booklets are printed in English, Spanish and Chinese. Here are PDFs for 1st-Grade Student Pages
Manipulatives have been provided to each site and should remain with the classroom. Here is a linked list of manipulatives for each grade Pre-Kindergarten through Grade 5.
Units
Unit Design
SFUSD units are designed around four tasks. These tasks offer all students opportunities to engage in meaningful and rigorous mathematics that allow for the development of the Standards for Mathematical Practice. These tasks give information about how students are learning the core concepts and skills of the unit.
All tasks are used for formative assessment—gathering information about what students know and are able to do—but they are not tests. The Entry, Apprentice, and Expert Tasks allow for student collaboration and individual accountability without being graded based on an expectation of mastery. The Milestone Task can be used as an individual assessment for grading students.
 |
|---|
- Entry Task: What do you already know?
- Apprentice Task: What sense are you making of what you are learning?
- Expert Task: How can you apply what you have learned so far to a new situation?
- Milestone Task: Did you learn what was expected of you from this unit?
Units
| Unit | Description | Orientation | |
|---|---|---|---|
| The first week of school is focused on setting up the classroom culture for the year and developing routines that support the development of the Standards for Mathematical Practice. Teachers will get to know their students as the students get to know themselves as math learners. | |||
| All whole numbers can be composed and decomposed into specific whole number combinations. These combinations can be shown visually in a variety of ways and recorded with an equation. These combinations are commutative. The Make Ten strategy is a useful strategy for solving problems. | Unit 1.1 Orientation | ||
| Two-dimensional shapes with or without curved surfaces can be described, classified, and analyzed by their attributes. Students determine which attributes define a shape, such as number of sides and vertices, and which attributes to not, such as color or size. Students may use informal language to describe these attributes. | Unit 1.2 Orientation | ||
| Different situations suggest different addition strategies such as counting on, thinking about doubles or making a ten. Different situations can result in the same sum. The expressions that represent situations with the same sum are equal. This relationship can be recorded with an equal sign. | Unit 1.3 Orientation | ||
| Different situations suggest different subtraction strategies such as counting back, think addition or decomposing to ten. Different situations can result in the same difference. The expressions that represent situations with the same difference are equal. This relationship can be recorded with an equal sign. | Unit 1.4 Orientation | ||
|
Unit 1.5: Measuring Length and Time New - Time |
Some attributes of objects are measurable and can be quantified by counting iterated units. | Unit 1.5 Orientation | |
| Addition and subtraction represent a relationship between quantities in a real world context. The context may represent an add to, take from, put together, take apart, or comparison situation which can be recorded symbolically with an equation. Any number in the relationship may be unknown. | Unit 1.6 Orientation | ||
| Three-dimensional objects (solids) with or without curved surfaces can be described, classified, and analyzed by their attributes, including faces, edges, and vertices. | Unit 1.7 Orientation | ||
| Addition and subtraction represent a relationship between quantities in a real world context. The context may be an add to, take from, put together, take apart, or comparison situation. Any number in the relationship may be unknown. This relationship can be recorded symbolically with an equation. | Unit 1.8 Orientation | ||
| The base ten numeration system is a scheme for recording numbers using the digits 0 through 9, groups of ten, and place value. For any number, the place of a digit tells how many ones, tens, hundreds, and so forth are represented by that digit. | Unit 1.9 Orientation | ||
| Organizing data can make it easier to collect and interpret. | Unit 1.10 Orientation | ||
| Each number has a word and a symbol that corresponds to its quantity. Quantities can be sequenced and compared. The focus of this unit is on discovering the base ten pattern of the counting numbers. (10 days) |
Lesson Structure and Core Math
|
LAUNCH |
The Launch of a lesson or task is a brief hook that might relate to previous learning, establish an inquiry question, or connect to real-world situations or interests. It will also support students to understand what is being asked of them, which may include guidance on the use of materials such as manipulatives. |
|
Key Questions How can you connect to students' interests/lives (hook)? |
|
|
EXPLORE |
During the Explore part of a lesson or task, students carry the cognitive load. Students experiment together with the most important math of each unit to develop, deepen and secure their mathematical understanding. They represent their thinking with numbers, pictures, words, and visual representations such as ten frames or number lines. Students are talking throughout this part of the lesson, and building on each other’s ideas and questions. The Explore often includes a math game and/or centers. |
|
Key Questions What are students doing? What work do you want to highlight? What does their work show about what they understand? What language are the students using to describe their work? |
|
|
SUMMARIZE |
During the Summarize part of a lesson or task, the teacher facilitates a conversation where students share what they have learned related to the core math. They notice and name similarities, differences, or connections across several different pieces of math work. A summary often, but not always, includes routines for consolidation of learning, such as a gallery viewing or individual reflection in a notebook. |
|
Key Questions How will you sequence the work to elicit peer-to-peer academic discourse? What questions or prompts might you use? How will you connect different pieces of work to each other? How will you connect the work to the core math? |
Planning Guide
This calendar is intended as an instructional guide to help with year-long planning. There is no expectation that you teach a particular lesson on a particular day. Each unit is set within a “window” of time that gives you some flexibility.
Reflection Questions Link to this section
- How are students' developmental needs, communities, and experiences being reflected and honored, or how could they be?
- What opportunities do you see for developing equitable access & demand, inquiry, collaboration, and assessment for learning?
- What are the implications for your own practice? What strengths can you build upon? What will you do first?
Want More?
Standards
More Resources
- The SFUSD Math Core Curriculum First-Grade Overview includes the priority standards, the scope and sequence of units and standards, the unit design, class norms, key instructional strategies, and icons used throughout the curriculum to support planning.
- 1st Grade Math Portal
- K-2 Combined Grade Portal
- Assessment resources (in addition to the embedded formative assessment in the Core Curriculum)
Contact the Math Team:
This page was last updated on May 18, 2023

